creatorcas.blogg.se - What is not a linear regression equation example

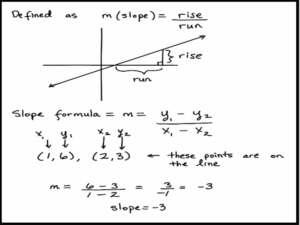
Linear regression is defined as a linear relationship between the response variable and predictor variables.

Why is a t-test used in the linear regression model?.

They allow you to build any model that you can imagine. In a next post we will see how to go beyond non-linear least square to embrace maximum likelihood estimation methods which are way more powerful and reliable. That was a bit of a hassle to get from the SSlogis parametrization to our own, but it was worth it! Lets plot it: lines(times,predict(m),col="red",lty=2,lwd=3) Residual standard error: 49.01 on 48 degrees of freedomĪchieved convergence tolerance: 1.537e-06 Fit non-linear least squaresįirst example using the Michaelis-Menten equation: #simulate some data

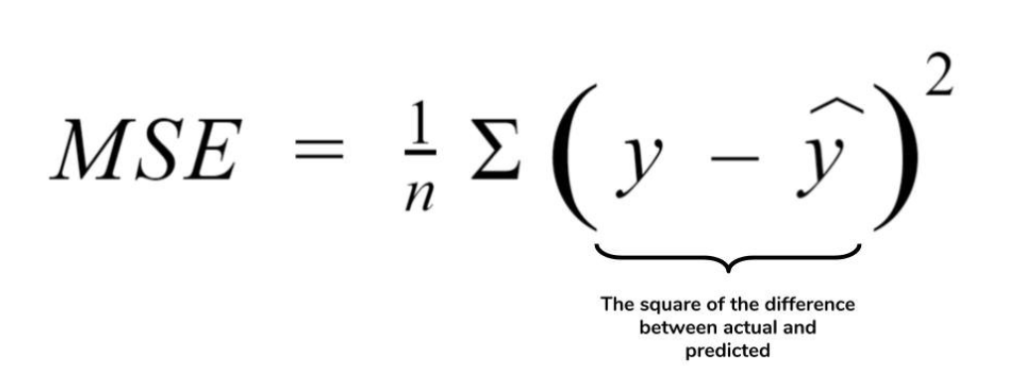
A nice feature of non-linear regression in an applied context is that the estimated parameters have a clear interpretation (Vmax in a Michaelis-Menten model is the maximum rate) which would be harder to get using linear models on transformed data for example. The most basic way to estimate such parameters is to use a non-linear least squares approach (function nls in R) which basically approximate the non-linear function using a linear one and iteratively try to find the best parameter values ( wiki). In non-linear regression the analyst specify a function with a set of parameters to fit to the data. As you may have guessed from the title, this post will be dedicated to the third option. In this case one may follow three different ways: (i) try to linearize the relationship by transforming the data, (ii) fit polynomial or complex spline models to the data or (iii) fit non-linear functions to the data. It is sometime fitting well to the data, but in some (many) situations, the relationships between variables are not linear. Drawing a line through a cloud of point (ie doing a linear regression) is the most basic analysis one may do.